【カジノ戦略】モンテカルロ法の使い方は?初心者にもわかりやすく解説!

「モンテカルロ法」または「モンテカルロ・シミュレーション」とは、乱数を用いて何らかの数値を算出する計算方法の1つです。

経済や金融、自然科学やテクノロジー、そしてギャンブルの戦略にいたるまで幅広い分野で応用されています。主にカジノやオンラインカジノのギャンブルで使われることが多いです。

今回はそんなモンテカルロ法についてわかりやすく解説しながら紹介していきたいと思います。

わかりやすく解説するモンテカルロ法①：モンテカルロ法とは

モンテカルロ法とは物事における不確実性やリスクの影響を分析・評価することで、起こり得る様々な結果の確率をモデル化する計算手法のことです。わかりやすく言えば、膨大なパターンのシミュレーションを行って物事の結果を予測する手法で、「モンテカルロ・シミュレーション」や「モンテカルロ実験」と呼ばれることもあります。

前述の通り、モンテカルロ法は様々な分野で広く使われており、解を導き出すのが困難な問題においてランダムなパターンのシミュレーションによって解の近似値を算出します。

モンテカルロ法の応用例

ギャンブル

一般的には、優秀なベッティングシステムの1つとして知られているが、カジノ側がゲームのペイアウト率を設定したり、プレイヤーがゲームの結果予測や長期的な利益を見積もったりする際にも使用。

気候・金融市場

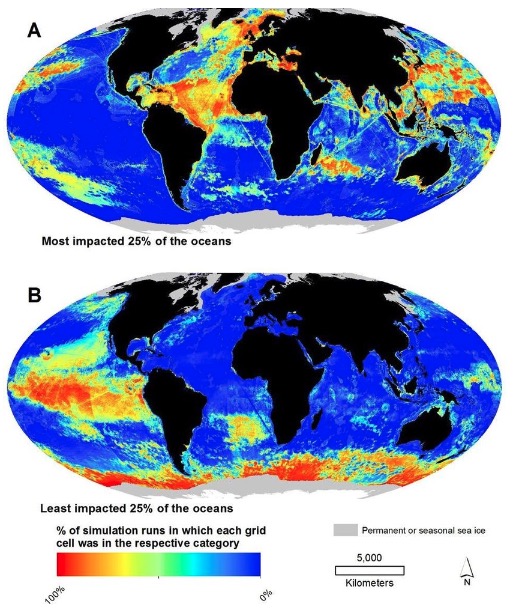
不確定要素が複雑に関連している気候や金融市場などで、将来起こり得る結果予測やリスク分析のシミュレーションに使用。

自然科学・テクノロジー

原子力の研究や原爆の開発、電子回路の設計、デジタル画像処理、機械学習アルゴリズムなどに使用。

わかりやすく解説するモンテカルロ法②：誕生の背景

モンテカルロ法は、モナコ公国にあるカジノで有名な地区の「モンテカルロ」がその名前の由来です。スロットやルーレットのように「ランダム要素」と「確率」が重要な意味を持ちます。

初期のモンテカルロ法は円周率の計算に使われたと言われています（等間隔で床に引かれた平行線に針を落とし、交差頻度から円周率の近似値を求めた）。物理学者のエンリコ・フェルミも1930年代に中性子の研究で使っていたようです。

現代におけるモンテカルロ法が考案されたのは1940年代後半、米ロスアラモス国立研究所で原爆開発に携わっていたスタニスワフ・ウラムによるものでした。原爆開発において中性子の挙動を測定するため、同僚のジョン・フォン・ノイマンの協力も得ながらこの手法を確立しました。

わかりやすく解説するモンテカルロ法③：モンテカルロ法の仕組み

モンテカルロ法は統計的なアプローチで不確実な物事における解を導き出します。シミュレーション分析では確立変数の影響により、起こり得る結果の範囲を予測するのに時間がかかってしまうことが1つの課題ですが、モンテカルロ法ではランダムなシミュレーションを多数行い結果を平均化します。モンテカルロ法におけるシミュレーションをわかりやすくすると以下のような流れです。

わかりやすく解説するモンテカルロ法④：ギャンブルの結果予測に使われるモンテカルロ法

ギャンブルにおけるモンテカルロ法には2つのタイプがあります。1つはゲームで特定の結果が起こる確率を予測するために使われるモンテカルロ法です。わかりやすく例を挙げると、ブラックジャックやポーカーで手持ちのカードから勝率を予測して次のアクションを判断したり、スポーツベッティングで試合結果のシミュレーションを行って、起こる確率が一番高い結果に賭ける際に使われます。

ギャンブルの結果予測でモンテカルロ法を使う際は以下の要素が重要になります。

上記に加え、利用可能なあらゆるデータも駆使してゲームに勝てる確率や利益を予測し、その結果をもとに適切なプレイ戦略を選んだりバンクロールを管理します。ただし、モンテカルロ法を使えば損失のリスクがゼロになるわけではなく、あくまで戦略やツールの1つとして活用するべきものであることは理解しておく必要があります。

メリット

• モンテカルロ法による分析データに基づいた意思決定ができる。
• モンテカルロ法で長期的な利益と損失の見込みがわかる。
• モンテカルロ法の結果を基にベストなプレイ戦略が選択できる。
• モンテカルロ法は様々なタイプのゲームに応用できる。

デメリット

• モンテカルロ法は100%の必勝法ではなく損失が出る可能性がある。
• モンテカルロ法のシミュレーションでは膨大な量の計算が必要になる。
• モンテカルロ法はランダム要素のないゲームや賭けでは使えない。
• モンテカルロ法には取り込めない不確定要素もあるため（プレイヤーの心理状況など）、結果の正確性は保証されない。
• モンテカルロ法以外の方法がより効率的な場合もある。

わかりやすく解説するモンテカルロ法⑤：ベッティングシステムとしてのモンテカルロ法

ギャンブルにおけるモンテカルロ法の2つ目の意味は、ベッティングシステムとしてのモンテカルロ法です。シミュレーションを用いた結果予測とは関係なく、一定の規則に基づいた数列を用いてベット額を増減させます。ギャンブルの世界ではモンテカルロ法というとこちらをイメージされる方が多いかもしれません。

わかりやすく解説するモンテカルロ法⑥：ベッティングシステムとしてのモンテカルロ法の使い方

ステップ1.　ベット額のベースとなる3つの数字を決める

ここで決めた3つの数字をベースに初回のベット額が決まります。数字はバンクロールの範囲で自由に選べますが、左から「1倍、2倍、3倍」となるようにしてください。ここではわかりやすく「1　2　3」を例にして説明していきます（単位：ドル）。

ステップ2.　3つの数字の一番左と右の合計を最後尾に加える

例の「1　2　3」でいうと「1 + 3 = 4」となり、数列「1　2　3」の最後尾に追加します。この「4」が初回ベット額になります。

ステップ3.　ゲームプレイ

4ドルのベット額でプレイします。ゲームに勝てばベット額は据え置きで次のゲームへ。負けた場合は次のステップに進みます。

ステップ4.　数列の一番左と右の合計を最後尾に加える

つまり「1 + 4 = 5」を数列「1　2　3　4」の最後尾に追加します。この「5」が次のベット額になります。

ステップ5.　ゲームプレイ

ここで負けた場合はステップ4に戻りますが、勝った場合は配当の倍率によって対応が変わります。

2倍配当の場合は数列に数字が3つ残っているため、上記の手順に従ってゲームを続行しますが、3倍配当の場合は数字が1つしか残っていないため、ここで数列をリセットして最初の状態から再度スタートします。

ベッティングシステムのモンテカルロ法では、このように数列の数字が残り1つになるか全て無くなった時点で最初の状態にリセットされます。その時の損益は以下の通りです。

数字がすべて無くなっている状態：2倍・3倍配当ともに必ずプラス

数字が残り1つの状態：3倍配当は必ずプラス。2倍配当はマイナスの場合がある

わかりやすくするため、モンテカルロ法を使ったゲームの結果を表にまとめてみます。

2倍配当のゲームの例

回数	数列	ベット額	結果	損益
1	1　2　3	$4	負け	-$4
2	1　2　3　4	$5	負け	-$9
3	1　2　3　4　5	$6	負け	-$15
4	1　2　3　4　5　6	$7	勝ち	-$1
5	2　3　4	$6	勝ち	+$11
6	3	–	–	+$11

数字が1つになったため6回目終了後は最初の数列に戻ります。このパターンでは損益がプラスで終了していますが、前述の通りマイナスになる場合もあります。

3倍配当のゲームの例

回数	数列	ベット額	結果	損益
1	1　2　3	$4	負け	-$4
2	1　2　3　4	$5	負け	-$9
3	1　2　3　4　5	$6	負け	-$15
4	1　2　3　4　5　6	$7	勝ち	+$6
5	3　4	$7	負け	-$1
6	3　4　7	$10	負け	-$11
7	3　4　7　10	$13	勝ち	+$2
8	–	–	–	+$2

数字がすべて無くなったため8回目終了後は最初の数列に戻ります。

ベッティングシステムとしてのモンテカルロ法は地道に利益を積み重ねていく低リスクな手法とされていますが、もちろんメリット・デメリットは存在します。

メリット

• モンテカルロ法はベット額が大幅に増える仕組みではないため、少額のバンクロールでも長くプレイできる。
• モンテカルロ法は損失のリスクを抑える「守り」の戦略の中では、勝った時に比較的大きな利益が出る。
• モンテカルロ法は長くプレイするほど損益が安定し損失のリスクが低くなる。

デメリット

• モンテカルロ法は勝敗によって数列を修正するので慣れるまで時間がかかる。
• モンテカルロ法は低リスクなベッティングシステムではあるものの、連敗が続けばベット額が大幅に上がる可能性がある。
• モンテカルロ法は地道に利益を積み重ねる手法なため、すぐに利益を出したいプレイヤー向きの戦略ではない。
• カジノによってはごく稀にモンテカルロ法などのシステムベットを禁止しているところがある。

わかりやすく解説するモンテカルロ法⑦：まとめ

以上、今回はモンテカルロ法についてわかりやすく解説してきましたが、最後に改めてポイントをまとめておきます。

モンテカルロ法は計算方法の1つで、ランダムなパターンのシミュレーションで物事の結果を予測する。

「モンテカルロ・シミュレーション」や「モンテカルロ実験」とも呼ばれ、経済や金融、自然科学やテクノロジー、そしてギャンブルなど幅広い分野で応用されている。

モンテカルロ法という言葉は、ギャンブルにおいては「ゲームの結果予測」と「ベッティングシステム」の2つを意味する。

ベッティングシステムとしてのモンテカルロ法は、数列を用いてベット額を増減させる手法。低リスクで地道に利益を積み重ねるのに適している。